Introduction to Geomlab - algebra with pictures
Geomlab is a programming utility developed at Oxford University to introduce new graduates to some of the ideas behind functional programming. Functional programming is an approach to computer programming that is very simple yet very powerful and Geomlab shows how it's done.
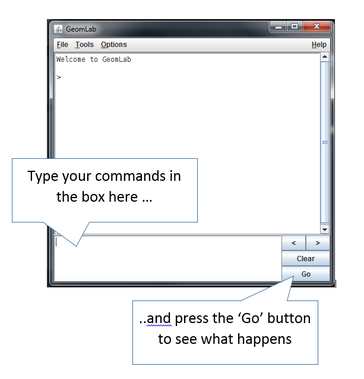
Find Geomlab on the K drive: Double-click to start
K:\Computing\geomlab\geomlab.jar
K:\Computing\geomlab\geomlab.jar
|
You should see the program run like this:
|
Try typing each of the following commands and press the 'Go' button
man What is the difference between the last two commands? Why are they different?
|
- the dollar sign '$' puts pictures side by side
- the ampersand '&' puts pictures on top of each other - their size is adjusted automatically
- there are rules for the order in which these are evaluated - $ is evaluated first, then & - just as multiplication is evaluated before addition
- we can override these ordering rules by using brackets
Click here for the Geomlab worksheets at Oxford University
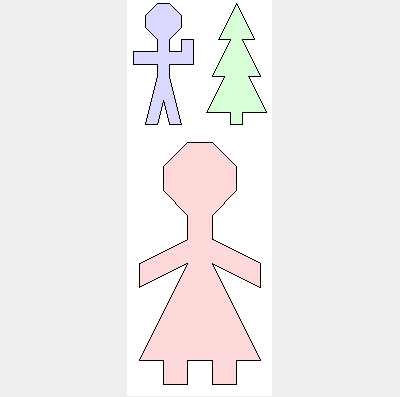
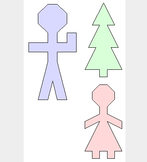
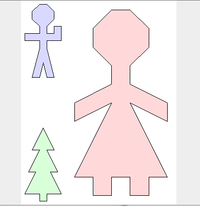
Some Geomlab puzzles - can you find the expression which creates them?
Each of these pictures can be created using only 'man', 'woman', 'tree' and 'blank' ('blank' puts in a blank space), plus the expressions & and $
|
|
|
|
|
Once you've found the answers - can you make a puzzle for the rest of the class? Create a picture and challenge your neighbour to reproduce it.
Taking it further....
Worksheet number two explains the Rot() function and shows how you can use it to create more complex shapes
Worksheet number three shows how to create functions within Geomlab
Worksheet number four introduces the power of recursion into functions, allowing repeated sequences of symbols
